Um antigo fragmento de tablete de argila datado de 3.700 anos atrás, durante o período da Antiga Babilônia, contém o que agora é o mais antigo exemplo conhecido de geometria aplicada, um matemático descobriu. Isso é mais de um milênio antes do nascimento de Pitágoras.
E esse artefato que alterou a história, conhecido como Si.427, estava em um museu em Istambul há mais de 100 anos.
“Si.427 data do período da Antiga Babilônia (OB) – 1900 a 1600 aC”, disse o matemático Daniel Mansfield, da Universidade de New South Wales (UNSW), na Austrália.
“É o único exemplo conhecido de documento cadastral do período OB, que é um plano usado por agrimensores para definir os limites do terreno. Neste caso, ele nos diz detalhes jurídicos e geométricos sobre um campo que foi dividido depois que parte dele foi vendido . “
Esse plano usa conjuntos de números conhecidos como triplos pitagóricos para derivar ângulos retos precisos ou conjuntos de números que se ajustam a modelos trigonométricos para calcular os lados de um triângulo retângulo. Isso torna o momento do artefato particularmente interessante, com implicações importantes para a história da matemática, observou Mansfield.
A descoberta é descrita em um novo artigo que analisa o contexto deste tablet com descobertas recentes sobre um tablet contemporâneo de Si.427, conhecido como Plimpton 322. Em 2017, Mansfield e colegas revelaram que Plimpton 322 era uma das primeiras tabelas trigonométricas , mostrando um lista completa de triplos pitagóricos.
Na época, os pesquisadores não sabiam qual seria o propósito dessa lista. Agora, eles acham que pode ser um pouco posterior a Si.427 e conter apenas triplas pitagóricas que seriam relevantes para fazer medições retangulares do solo. Em outras palavras, é um manual de planejamento.
Isso está em contraste com a trigonometria apresentada por Pitágoras, que foi concebida olhando para as estrelas no céu no segundo século AEC. O número de triplos pitagóricos que podem ser usados para fazer medições de terra por agrimensores babilônios é muito pequeno.
Um triplo pitagórico se ajusta à equação a 2 + b 2 = c 2 , onde os lados que definem um triângulo adjacente ao ângulo reto são aeb, e a hipotenusa (o lado mais longo) é c. O exemplo mais simples seria 3 2 + 4 2 = 5 2 .
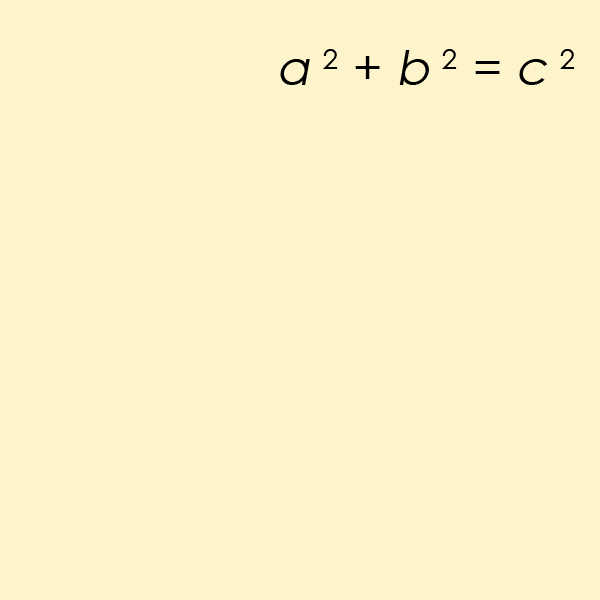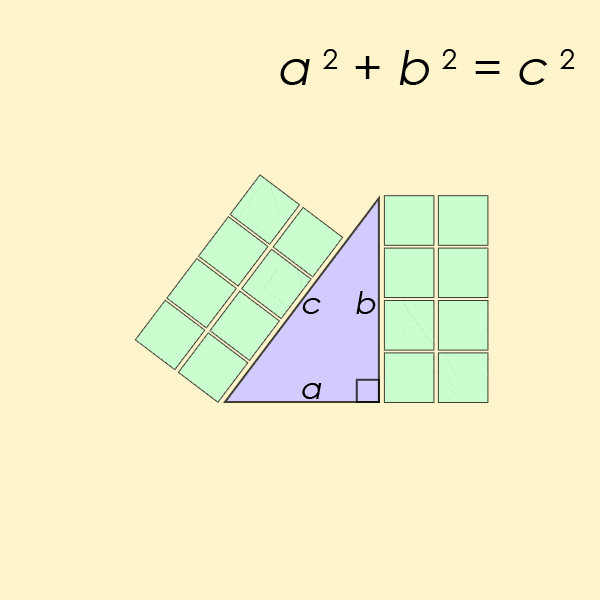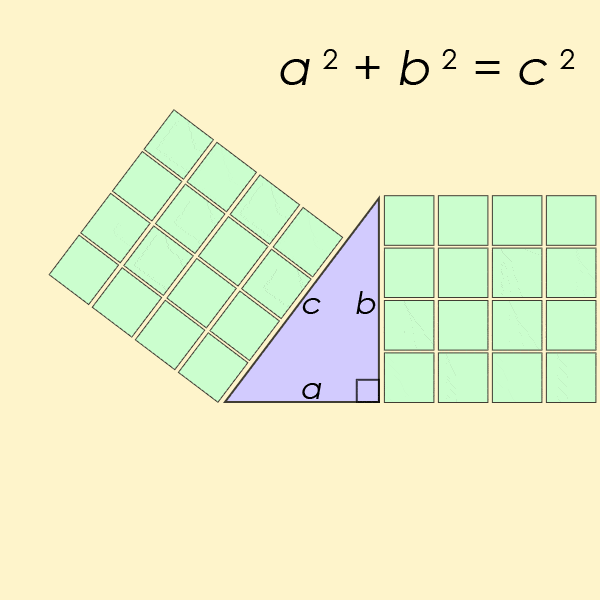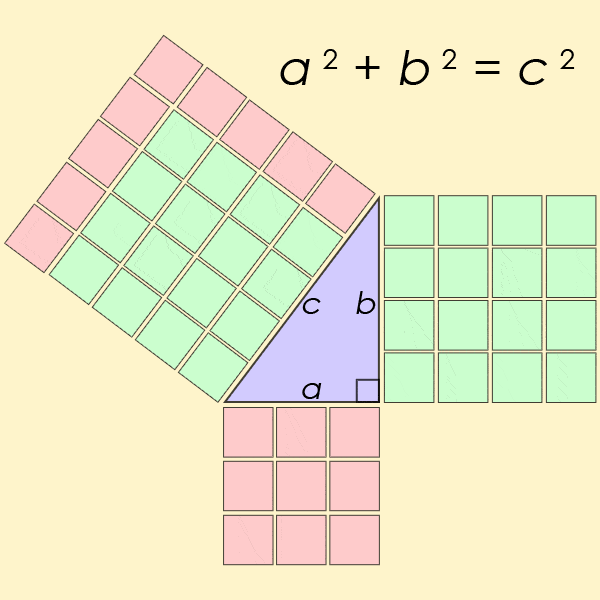
Esses conjuntos de números podem ser usados para desenhar triângulos e retângulos com ângulos retos perfeitos. Mas o sistema numérico babilônico sexagesimal, ou de base 60, dificultava o trabalho com números primos maiores que 5.
“Isso levanta uma questão muito particular – seu sistema de número de base 60 exclusivo significa que apenas algumas formas pitagóricas podem ser usadas”, disse Mansfield .
“Parece que o autor de Plimpton 322 passou por todas essas formas pitagóricas para encontrar essas formas úteis. Essa compreensão profunda e altamente numérica do uso prático dos retângulos recebe o nome de ‘prototrigonometria’, mas é completamente diferente da nossa trigonometria moderna envolvendo sin, cos e tan. “
Agora, com o Si.427, finalmente sabemos para que eles queriam usar essas triplas pitagóricas – estabelecer limites de terra, de acordo com Mansfield.
“Isso vem de um período em que a terra está começando a se tornar privada – as pessoas começaram a pensar na terra em termos de ‘minha terra e sua terra’, querendo estabelecer um limite adequado para ter relações positivas de vizinhança” , explicou .
“E isso é o que este tablet diz imediatamente. É um campo sendo dividido e novos limites são feitos.”
Outros comprimidos desse período revelam por que isso era tão importante. Uma delas diz respeito a uma disputa por tamareiras na fronteira entre duas propriedades, na qual o administrador local concordou em enviar um agrimensor para resolver o assunto. É fácil ver por que a capacidade de medir com precisão lotes de terra pode ter sido importante.
No entanto, demonstra uma compreensão sofisticada da geometria. Pode não ter sido tão avançado quanto a trigonometria mais tarde descrita pelos gregos antigos, mas sugere que nossa compreensão da matemática pode ter sido mais incremental do que o conhecimento histórico atual nos diz.
“Ninguém esperava que os babilônios estivessem usando os triplos pitagóricos dessa forma”, disse Mansfield . “É mais semelhante à matemática pura, inspirada nos problemas práticos da época.”
A pesquisa foi publicada em Foundations of Science
Animação mostrando o exemplo mais simples de triplos pitagóricos. (AmericanXplorer13 / Wikimedia / CC BY-SA 3.0)

